Home Coding Leetcode Medium

⭐️⭐️

# 題目敘述

Given a directed acyclic graph, with n vertices numbered from 0 to n - 1 , and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi .

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

# Example 1

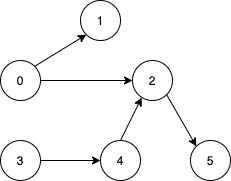
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It’s not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

# Example 2

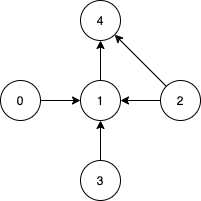
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

# Solution

class Solution {
public:
    vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {
        unordered_set<int> s;
        for (vector<int>& edge : edges) {
            s.insert(edge[1]);
        }
        vector<int> res;
        for (int i=0; i<n; i++) {
            if (s.find(i) == s.end()) {
                res.push_back(i);
            }
        }
        return res;
    }
};
class Solution {
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
        Set<Integer> link = new HashSet<>();
        for (List<Integer> edge : edges) {
            link.add(edge.get(1));
        }
        
        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (!link.contains(i)) {
                ans.add(i);
            }
        }
        
        return ans;
    }
}